Le théorème de Pythagore est un théorème de géométrie euclidienne qui doit son nom à Pythagore de Samos, philosophe de la Grèce antique du VIème siècle avant J.C, mais dont le résultat était déjà connu depuis -300 par Euclide qui en fit la démonstration la plus ancienne. Il est utilisé dans de nombreux domaine comme l’architecture, l’ingénierie, etc.
I. Le théorème de Pythagore
A. La théorie
Ce théorème permet de calculer l’une des longueurs d’un côté par rapport aux longueurs des deux autres côtés. Mais seulement lorsque le triangle est dit triangle-rectangle.
La première condition pour que ce théorème s’applique est donc que mon triangle soit rectangle.
Comment définir que mon triangle est un triangle-rectangle ? Il faut que l’un des trois angles soit un angle droit soit un angle à 90°.
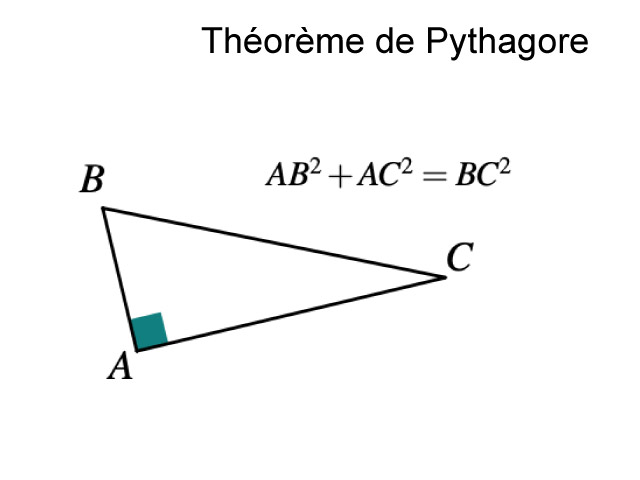
La phrase de justification est souvent sous cette forme : « Si un triangle est un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés ». Moyen mnémotechnique, l’hypoténuse correspond toujours à la plus grande longueur, formé par les deux lettres qui ne sont pas un angle droit. Ainsi, si nous savons que le triangle est rectangle en B, l’hypoténuse est forcément AC.
B. Mise en application
Exemple 1 :
Soit AMZ le triangle rectangle en M tel que AM = 4,8cm et MZ = 3,6 cm. Il faut calculer AZ qui est ici l’hypoténuse.
Le théorème s’applique car le triangle est un triangle rectangle dont nous connaissons la longueur de deux côtés.
Rédaction :
D’après le théorème de Pythagore, comme AMZ est un triangle rectangle en M alors AZ² = AM² + MZ²
Soit AZ² = 4,8²+3,6²
AZ² =23,04 + 12,96
AZ² = 36
Donc AZ = √36 = 6
La longueur du côté AZ est donc de 6 cm.
Exemple 2 :
Dans cet exemple, le triangle rectangle EFG à son angle droit en F tel que EF = 12 cm et EG = 13 cm. Il faut calculer FG qui cette fois-ci n’est pas le côté opposé à l’angle (l’hypoténuse), mais le processus reste sensiblement le même. On écrit toujours la formule de base en premier qui commence par l’hypoténuse pour éviter de se tromper, si on a un doute, avant d’interchanger quand le côté à calculer n’est pas l’hypoténuse.
Rédaction :
D’après le théorème de Pythagore, comme EFG est un triangle rectangle en F alors EG²= EF² + GF².
Soit 13² = 12²+FG²
169 =144 + FG²
169 – 144 = FG²
FG² = 25
FG =√25 = 5
La longueur du côté FG est de 5 cm.
II. La réciproque du théorème de Pythagore
A. La théorie
Elle permet de définir que si le carré de l’hypoténuse est égal à la somme des carrés des longueurs des autres côtés alors le triangle est bien un triangle rectangle dont l’un des angles est à 90° soit un angle droit.
On l’énonce souvent de cette façon : « Si dans un triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et son hypoténuse est le plus grand côté. »
B. Mise en application
Exemple 1 :
Soit AMZ, un triangle avec AM = 4,8cm, MZ = 3,6 cm et AZ = 6cm. Ce triangle est-il rectangle ?
Rédaction :
Tout d’abord, il faut définir où se trouverait l’angle droit : l’angle opposé au côté le plus long, soit M qui est l’angle à l’opposé de AZ.
D’après le théorème de Pythagore, AMZ est un triangle rectangle en M si et seulement si AZ² = AM² + MZ²
Soit AZ²= AM²+MZ²
6² = 4,8²+3,6²
36 =23,04 + 12,96
36 = 36
Donc le triangle AMZ est bien un triangle rectangle en M.
Exemple 2 :
Soit EFG, un triangle avec EF = 12cm, EG = 13cm et FG = 6cm. Ce triangle est-il rectangle ?
Rédaction :
La plus grande longueur est EG donc si le triangle est rectangle, il le sera sur l’angle F.
D’après le théorème de Pythagore, EFG est un triangle rectangle en F si et seulement si EG²= EF² + GF².
Soit 13² = 12²+6²
169 =144 + 36
169 ≠ 180
Donc le triangle EFG n’est pas un triangle rectangle car EG²≠EF²+GF²